Árboles binarios de búsqueda (BST)
En esta sección vamos a ver las operaciones típicas que se pueden realizar en un árbol binario de búsqueda (BST).
Inserción de datos
La inserción de datos en un BST es un proceso fundamental que se basa en comparar los valores de los nodos para mantener la estructura del árbol ordenada.
El proceso de inserción es el siguiente:
- Comienzo con el nodo raíz: Si el árbol está vacío, el nuevo nodo se convierte en la raíz del árbol.
- Comparación: Si el árbol ya tiene nodos, comienza por la raíz y compara el valor del nuevo dato con el valor del nodo actual.
- Desplazamiento a la izquierda o a la derecha:
- Si el valor del nuevo dato es menor que el valor del nodo actual, desplazas la comparación hacia el subárbol izquierdo.
- Si el valor del nuevo dato es mayor que el valor del nodo actual, desplazas la comparación hacia el subárbol derecho.
- Nodo hoja: Continúas comparando y desplazando hacia la izquierda o derecha hasta llegar a un nodo hoja.
- Inserción: Se añade el nuevo nodo como hijo del nodo hoja en la posición adecuada (izquierda o derecha, según la última comparación).
Recorridos
Los recorridos de los BST son técnicas para visitar todos los nodos del árbol de diferentes maneras.
Estos recorridos son útiles para realizar operaciones como listar elementos, buscar datos y modificar la estructura del árbol.
Los tres principales tipos de recorridos para árboles binarios son:
- Preorden
- Inorden
- Postorden
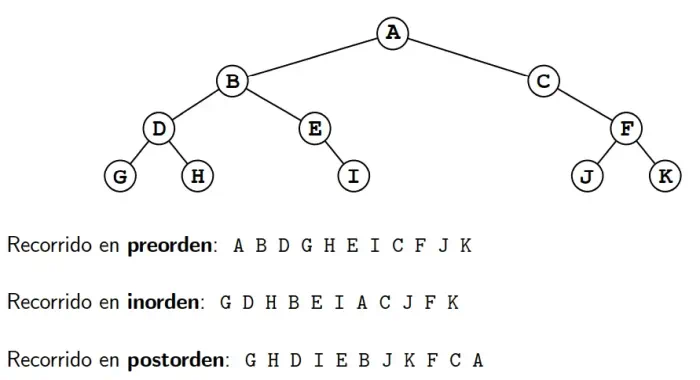
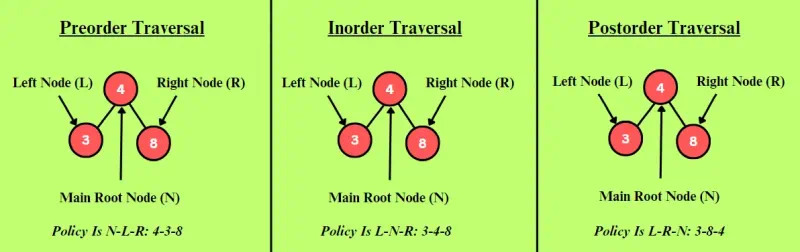
Recorrido preorden
El recorrido preorden (preorder) es útil cuando se necesita procesar la raíz antes de sus nodos hijos.
Algunos ejemplo de uso son:
- Copia o clonación de un árbol: Como se procesa primero la raíz, luego el hijo izquierdo y después el derecho, es muy útil para reconstruir un árbol en otra estructura de datos.
- Guardar un árbol en disco o transmitirlo: Si se almacena en preorden junto con información de nodos vacíos, se puede reconstruir exactamente el mismo árbol después.
- Evaluación de expresiones (árboles de expresión): En árboles binarios que representan expresiones matemáticas, el preorden genera la notación prefija (o polaca).
El recorrido preorden visita los nodos del árbol en el siguiente orden:
- Imprimir nodo raíz
- Consultar subárbol izquierdo
- Consultar subárbol derecho
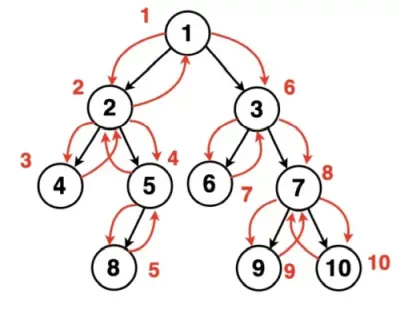
El resultado del recorrido es: 1-2-4-5-8-3-6-7-9-10
Recorrido Inorden
El recorrido inorden (inorder) es útil en árboles binarios de búsqueda (BST) porque visita los nodos en orden ascendente.
El uso principal del recorrido inorden es obtener los elementos de un BST de forma ordenada.
El recorrido inorden visita los nodos del árbol en el siguiente orden:
- Consultar subárbol izquierdo
- Imprimir nodo raíz
- Consultar subárbol derecho
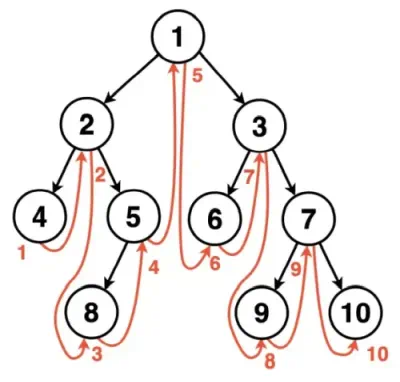
El resultado del recorrido es: 4-2-8-5-1-6-3-9-7-10
Recorrido Postorden
El recorrido postorden (postorder) es útil para procesos que necesitan asegurar que se procesen todos los nodos hijos antes de procesar la raíz.
Algunos ejemplo de uso son:
- Eliminar un árbol o liberar memoria: Para borrar un árbol, primero debes eliminar los hijos y luego el nodo padre.
- Evaluación de expresiones: En árboles de expresión matemática, postorden permite calcular primero los operandos y luego aplicar el operador.
- Procesamiento de dependencias: En problemas tipo “dependencias de tareas”, postorden garantiza que se procesen primero las tareas dependientes antes de la tarea principal.
El recorrido postorden visita los nodos del árbol en el siguiente orden:
- Consultar subárbol izquierdo
- Consultar subárbol derecho
- Imprimir nodo raíz
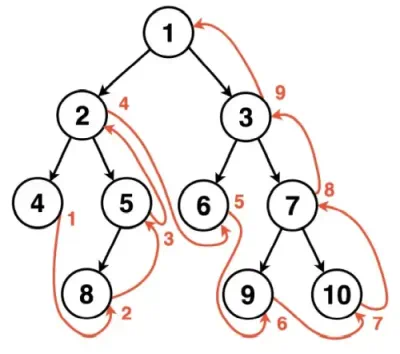
El resultado del recorrido es: 4-8-5-2-6-9-10-7-3-1